Twee superbelangrijke concepten die je vast al hebt gehoord: differentiëren en integreren. Wat is dat?
Wat is Differentiëren?
Differentiëren is een manier om de snelheid van verandering te meten. Stel je voor dat je op een skateboard zit en je vaart hard. Hoe snel ga je nu? Dat is het idee van differentiëren! Het helpt ons om te begrijpen hoe dingen veranderen.
Bijvoorbeeld, als je een functie hebt zoals:

Dan is de eerste afgeleide, wat we krijgen door te differentiëren,
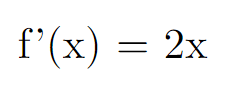
Dit betekent dat als jij een beetje dichterbij kijkt naar de waarde van \(x\), je kunt zien hoe snel \(f(x)\) verandert. Cool, toch?
Oké quizvraag: stel f(x) zegt hoe snel ik van een heuvel ga met m’n skateboard, en x is seconden. Hoe hard ga ik dan na 1 seconde?
Precies! 2 m/s, want f’(1) = 2*1 = 2.
Dus hoe hard ga ik na 4 seconden?
Precies! 8 m/s want f'(4) = 2*4 = 8
De eerste afgeleide heeft je dus de verandering in f(x) in punt x. Dat is wat algemener, maar je kunt altijd terugdenken aan dat skateboard en snelheid 😉.
En Wat is Integreren?
Integreren is eigenlijk het tegenovergestelde van differentiatie. Het is als het terugvinden van de originele functie. Stel je voor dat je al die kleine stukjes van iets bij elkaar optelt om de totaalwaarde te krijgen. Dit is handig als je wilt weten hoeveel je in totaal hebt.
Bijvoorbeeld, als je de afgeleide hebt:
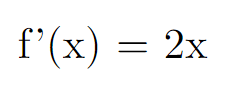
En je wilt de oorspronkelijke functie vinden, dan moet je integreren:
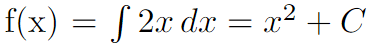
Hoe doe je dat? Dat lees je in deze blog
Waarom zijn ze Belangrijk?
Zonder differentiëren en integreren zouden veel dingen in de natuurkunde, economie en zelfs in je dagelijkse leven niet te begrijpen zijn. Dus, volgende keer als je wiskunde hebt, onthoud dat deze twee concepten niet alleen nummers en symbolen zijn; ze zijn sleutels tot een wereld vol mogelijkheden!
Dus, pak je wiskundeboek en ga aan de slag! Veel succes!




